Webpages about Smoldyn and spatial simulation
- Brief description of Smoldyn
- Spatial simulation and simulators
- Comparison table of particle-based simulators
- Questions and answers about Smoldyn
- Advice on choosing simulation parameters
- Research project ideas
- Algorithm details
Page contents
- The importance of biological modeling
- What methods are available for spatial stochastic simulation?
- What software is available for particle-based simulation?
The importance of biological modeling
Why model biology with simulations?
Science has always progressed through a comination of experiments and model building. Experiments provide new information and models help make sense of that information. As our understanding of cell biology deepens, and as experiments are able to measure more detail, the models need to reflect this increased complexity. Computer simulations are helping address this need. They contribute in four primary ways (Mogilner, 2005):
- To quantify experimental data
- To efficiently test hypotheses
- To deepen our understanding of individual systems
- To help us understand how multiple systems interact
Why might I need spatial simulations?
Simply put, everything in cell biology is highly spatially organized, and this organization is essential for life. Although much can be learned about biology while ignoring this organization, many other essential aspects can only be understood by building spatial models.
Why might I need stochastic simulations?
Stochastic effects tend to important in biology when there are relatively few individual molecules of a particular species and their exact number is not controlled perfectly (as it is with chromosomes). For example, suppose DNA is transcribed to about 25 mRNA transcripts. This number will tend to vary by about its square root, which is 5 transcripts, or 20% in this case. Translation of RNA to protein maintains this 20% variability, and adds a little more. This stochastic gene expression underlies a large fraction of the cell-to-cell variability that is observed. If it is the only significant source of stochasticity in some system, then non-spatial stochastic simulation methods are typically adequate (e.g. the Gillespie algorithms).
Stochasticity also tends to be important when investigating spatial effects. This is because the study of spatial phenomena necessarily involves focusing on small volumes of space, and there are often relatively few individual molecules in small spatial volumes. In addition, many important biological processes depend on multimeric protein complexes. These are clearly composed of integer numbers of individual proteins, which can be captured by stochastic models but not by continuous models.
What methods are available for spatial stochastic simulation?
Spatial stochastic simulation methods can be divided into two classes.
Top-down approach: spatial Gillespie methods
In the top-down approach, one starts with simple non-spatial non-stochastic mass action kinetics, described as a system of ordinary differential equations, and then adds detail to these methods. Stochastics are typically added in by using one of the Gillespie algorithms. Space is typically added in by partitioning the system volume using a coarse grid, in which each cell contains many individual molecules. Other volume meshing methods can be used, too. Finally, one can combine the stochastic and spatial methods by running the Gillespie algorithm within each spatial partition, leading to what is often called the spatial Gillespie method. In this case, diffusion between cells is represented using the same formalism as reactions.
Bottom-up approach: particle-based simulation
In the bottom-up approach, one starts with the underlying physics of the system of interest and then approximates them to make a model that is sufficiently tractable. For particle-based simulation, as Smoldyn does, the approximations include: treating water molecules and other molecules that are not of immediate interest implicitly, ignoring molecular structure detail, ignoring molecular orientations, and often ignoring excluded volume interactions between modeled molecules. These approximations are well justified for a wide variety of models, although, of course, they do affect results and so may need to be considered carefully.
Particle-based simulators include fixed time-step simulators, including ChemCell, MCell, and Smoldyn. In all of these, the simulator computes the changes that happen during the course of a time step based on the situation at the beginning of the time step. This involves approximations, but becomes increasingly accurate as time steps are reduced (at the cost of slower simulations). Alternatively, Green's Function Reaction Dynamics (GFRD) is a particle-based method that uses event-based time steps. Here, the system steps from one event to the next, where a typical event is a collision between two molecules or a molecule-surface interaction. Because only one event happens per time step, GFRD is more accurate than fixed-time step simulators, but it is also much more computationally intensive for typical simulations. It is also much more difficult to implement.
Comparison between the methods
Spatial Gillespie methods are typically faster than particle-based methods (by a factor of 2 in a direct test by Dobrzynski et al.), making them better for faster simulations and for larger systems. They are also particularly useful when one is adding detail to an existing ODE or PDE model because it is possible to add detail in a sequential manner and hence never break the model during the conversion process. On the other hand, particle-based methods tend to be more accurate. Particle-based methods are also more flexible. For example, they enable users to define complex membrane geometries with a wide-range of molecule-surface interactions. During the few years, we hope to add filament support to Smoldyn, which would be very difficult to accomplish with spatial Gillespie methods.
For more details
Here are a review article and a primer that colleagues and I wrote on these topics:
- Andrews, Steven S., Tuan Dinh, and Adam P. Arkin. "Stochastic models of biological processes" Encyclopedia of Complexity and System Science, Meyers, Robert (Ed.) Volume 9:8730-8749. Springer, NY, 2009. pdf
- Andrews, Steven S. and Adam P. Arkin. "Simulating cell biology." Curr. Biol. 16:R523, 2006. pdf
What software is available for particle-based simulation?
Simulator citations
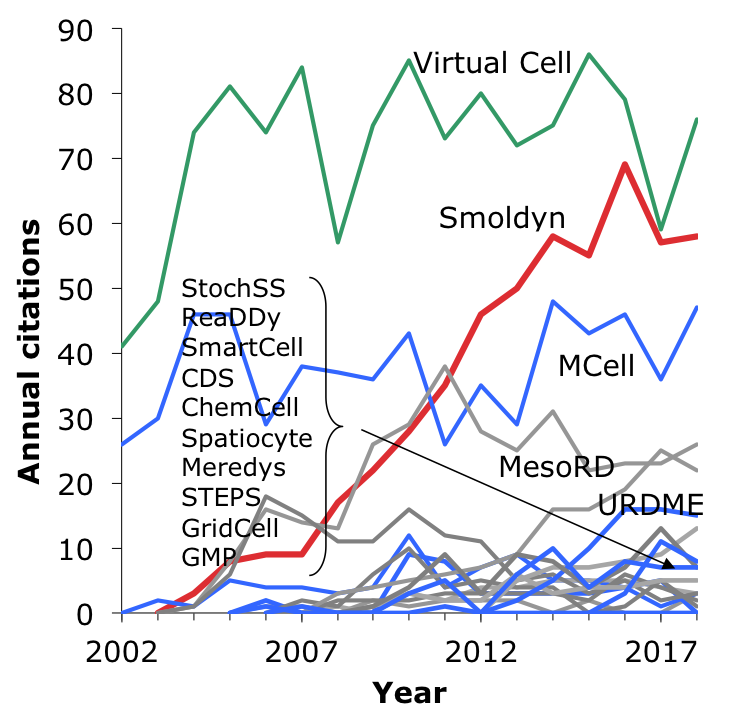
|
This figure shows annual citations to different software packages, from Google scholar. The red line represents Smoldyn, blue lines represent other particle-based simulators, the green line represents Virtual Cell (originally a PDE-based simulator, but now a hybrid simulator that uses Smoldyn for its particle-based simulations), and the grey lines represent spatial Gillespie simulators. |
MCell
MCell was the first major program for particle-based simulation, introduced in 1991 by Joel Stiles and Tom Bartol. It is still excellent software that offers a wide variety of excellent features. It offers better graphics than Smoldyn does, some aspects of its input format are easier to use, and it is available as pre-compiled code for a wider variety of computers. MCell has been particularly widely used in the neural signaling community.
Smoldyn
Smoldyn was written by Steve Andrews, with a first release in 2004. We feel that Smoldyn has largely caught up to, and in many ways surpassed, MCell at this point. Smoldyn runs about twice as fast as MCell and offers substantially more accurate reaction and surface interaction algorithms. Smoldyn also offers many unique features, including a wide variety of run-time commands that the user can choose from, real-time graphical output, and multiple geometric primitives. Smoldyn tends to be the preferred program among people doing quantitative biophysics research.
ChemCell
ChemCell was written by Steve Plimpton, also releasing in 2004. ChemCell has not seen substantial development progress for many years. It supports many fewer features that MCell or Smoldyn.
Meredys
Meredys was a brief effort by Dominic Tolle and Nicolas Le Novère. It focused on macromolecular complexes, which remain a weak point of other simulators. However, Meredys has relatively few other features and is not being developed actively.
Cellular Dynamic Simulator (CDS)
CDS is a new arrival to the particle-based simulator scene, with its first publication in 2010, by Byrne, Waxham, and Kubota. We have not used CDS nor spoken to the authors about it, so we don't know any more than what their paper describes. Whereas the other particle-based simulators use fixed time steps, CDS uses event-based time steps that are similar to but different from those of GFRD. In principle, this should make it possible for CDS to be more accurate than the other simulators listed here (probably at the expense of some speed performance). However, the published tests are not very rigorous, so it is hard to assess its accuracy objectively. The CDS publication shows excellent graphics and reports that the software comes with a graphical user interface for model definition.
