2025 |
|

|
Ruan, S., R. He, Y. Liang, R. Zhang, J. Yuan
Journal of Molecular Biology 437:168920, 2025
In two-component signaling pathways, the phosphorylation of response regulator proteins and their subsequent diffusion
play pivotal roles in signal transmission. This study investigates the impact of protein phosphorylation on their
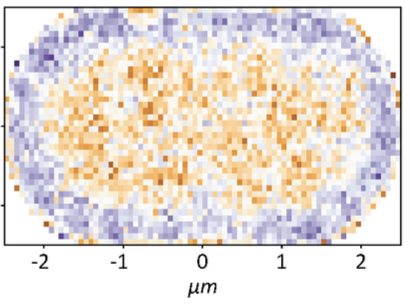
dispersion properties. They used the response regulator CheY, for bacterial chemotaxis, and measured its spatial distributions
and diffusion characteristics of both CheY and CheYp through single-molecule tracking within live cells. They found that
phosphorylation enhanced diffusion and mitigated the constraining influence of the cell membrane. Moreover, ATP-dependent
fluctuations also promoted protein diffusion and reduced the restraining effect of the cell membrane. These findings highlight
important effects of phosphorylation beyond protein activation.
|

|
Dingwell, D.A. and C.H. Cunningham
Magnetic Resonance in Medicine 93:369-383, 2025
The authors developed a novel particle-based magnetic resonance model and applied it to experimental designes that are
affected by the spatial organization of particles, including metabolic reaction kinetics, microstructural effects on
diffusion, and radiofrequency refocusing effects in gradient-echo sequences. They developed it by integrating a forward
solution of the Bloch equations with the Smoldyn simulator. The model accurately reproduced the reaction kinetics of
enzyme-mediated conversion of pyruvate to lactate. These results illustrate the model's capability to investigate
multifactorial signal dynamics such as those underlying hyperpolarized C-13 MRI data.
|
2024 |
|

|
Kilic, B.A. and O.B. Akan
ArXiv 2412.20161v1, 2024
Molecular Communication (MC) leverages the power of diffusion to transmit molecules from a transmitter to a receiver.
This paper proposes a novel modulation technique that encodes the information into the relative concentrations of multiple
molecules called Multi Ratio Shift Keying (MRSK), designed for diffusion-based MC. This approach can help mitigate the
effects of intersymbol interference and provides a flexible communication channel. They assessed MRSK performance both
analytically and through particle-based simulations under various channel conditions, identifying potential sources of error.
Comparison with other common modulation schemes showed that MRSK significantly outperforms all traditional modulation schemes.
|

|
Recouvreux, P., P. Pai, V. Dunsing, R. Torro, M. Ludanyi, P. Mélénec, M. Boughzala, V. Bertrand, P. Lenne
Current Biology 34:1853-1865, 2024
The authors used the Caenorhabditis elegans embryo to study how Wnt ligands, an evolutionarily conserved family of signaling
proteins, dynamically organize to establish cell polarity in a developing tissue. Wnt ligands are produced in the posterior
half of embryos and spread extracellularly to transmit information to target cells in the anterior half. With quantitative live
imaging and fluorescence correlation spectroscopy, they showed that Wnt ligands diffuse through the embryo over a timescale
shorter than the cell cycle, in the intercellular space, and outside the tissue below the eggshell.
The polarity established at the tissue level by a posterior Wnt source can be transferred to the cellular level. These results
support a diffusion-based long-range Wnt signaling, which is consistent with the dynamics of developing processes.
|

|
Losa, J., and M. Heinemann
Biophys. J. 123:1211-1221, 2024
The mobility of particles in the cytoplasm depends on factors such as concentration, shape, and physicochemical properties of
crowders. These authors combined experimental and computational approaches to determine the diffusion coefficient of a 40 nm
particle in the cytoplasm of E. coli after removal of different macromolecules in order to quantify the hindering effect of
each depleted macromolecule. They found the effects were of comparable magnitude for DNA, mRNA, and remaining macromolecules.
This work illuminates the interplay between intracellular composition and the physical properties of the cytoplasm at the 40 nm
scale. Smoldyn simulations were useful for calibrating their experimental observations.
|

|
Abdali, A., and M. Kuscu
IEEE Trans. on Communications 72:4564, 2024
Molecular Communication (MC) is a an engineered communication technology that is inspired by biological
systems in that diffusing molecules are used for information transfer. Using microfluidics and electronic
sensors (graphene field effect transistor biosensors), the authors designed a practical MC system. Models
provided insights into the dispersion and distortion of received signals, thus potentially informing the
design of new frequency-domain MC techniques. The model accuracy was verified through particle-based
spatial stochastic simulations.
|

|
Hladyshau, S., K. Guan, N. Nivedita, B. Errede, D. Tsygankov, T.C. Elston
Cells 13:1358, 2024
Cell polarization, the asymmetric distribution of proteins and other molecules within a cell, is the first step in many cellular processes.
These authors applied a multiscale modeling approach to examine the polarity circuit of yeast,
finding bistability and rapid dismantling of the polarity site following a loss of signal. This could be explained with an ODE model involving
positive and negative feedback acting on different time scales. That was expanded to a coarse-grained reaction-diffusion model, which explained
key features of the polarity circuit, and was expanded again to capture the biochemical reactions. That was converted to a particle-based model
that captured greater spatial detail, now with accurate stochastics. While these models assumed that negative regulation results from negative
feedback, experimental observations do not rule out the possibility that it could also occur through an incoherent feedforward
loop. They suggest how negative feedback might be distinguished from incoherent feedforward regulation.
|

|
Ahmed, Y.M. and G.R. Bowman
Nature Comm. 15:9282, 2024
Many bacterial species, including the C. crescentus bacterium investigated here, exhibit asymmetric cell division,
leading to the question of how the cell directs specific regulatory proteins to the correct cell poles. Curiously, both
poles contain a membraneless phase-separated microdomain, established by the polar assembly hub PopZ, through most of
the cell cycle, yet many of the proteins that depend on it exhibit unipolar and transient localization. Based on many
experimental observations, the authors hypothesized that the activity of the kinase/phosphatase protein CckA acts as a
switch that regulates PopZ's interaction several other proteins, and that this switch is controlled by a protein that
localizes to only one of the two cell poles. This hypothesis was confirmed by experiement and particle-based modeling.
|

|
Civas, M., M. Kuscu, O.B. Akan
IEEE Transactions on Communications 72:4741-4755 2024
Molecular Communications (MC) is a bio-inspired communication paradigm using molecules as information carriers.
Biosensor field-effect transistor (bioFET)-based architectures are promising MC receivers, having surface receptors
that undergo reversible reactions with ligands that are then converted into electrical signals via field effect.
These receivers have limited specificity to target ligands, which leads to molecular cross-talk from interfering ligands.
Decoding such interference is challenging in the time domain, so these authors introduce a frequency-domain detection
technique which exploits the distinct binding reaction rates of different ligand types. They analyze the bit error
probability, confirming its superior performance in various interference scenarios, and validated the theoretical
performance through particle-based simulations.
|

|
Ni, H. and O.B. Akan
ArXiv 2411.09787, 2024
This is a paper on molecular communication (MC), which is the design of engineered communication systems using diffusing
molecules as information carriers. The authors point out that MC in microfluidic channels is noisy due to the stochastic
nature of molecule propagation and dynamic noisy environments, which leads to high bit error rates and reduced communication
efficiency. They address this with ART-Rx, a novel Adaptive Real-Time Threshold Receiver for MC. It is implemented
within a conceptual system-on-chip and employs a Proportional-Integral-Derivative (PID) controller to dynamically adjust
the detection threshold. MatLab and Smoldyn simulations showed that their system significantly outperforms conventional methods.
|

|
Tran, B.M., C.M. Punter, D. Linnik, A. Iyer, B. Poolman
J. Mol. Biol. 436:168420, 2024
The periplasmic space of Gram-negative bacteria is only about 25-30 nm thick, which affects free diffusion of (macro)molecules.
The authors performed single-particle displacement measurements and diffusion simulation studies to investigate how this confinement
affects the apparent mobility of proteins in the Escherichia coli periplasm. They found fast and slow diffusion components, where the
fast fraction represents normal diffusion within this confinement space, and the slow component represents proteins that are hindered
by large periplasmic structures. The figure shows individual diffusive trajectories.
|
2023 |
|
|
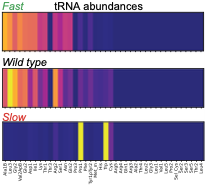
Maheshwari, A.J., J. Calles, S.K. Waterton, D. Endy
Nature Comm. 14:4594, 2023
The authors used a modified version of Smoldyn to predict how tRNA abundances impact protein synthesis rates.
Using rational design and direct RNA synthesis, they then made 21 synthetic tRNA surrogates from scratch and used
a computer aided design framework to engineer translation systems that were predicted to work faster or slower.
Wet lab tests of the synthetic systems showed qualitative agreement with predictions. This shows that first
principles modeling combined with experiments can be used for rational design in synthetic biology.
|
|
Recouvreux, P., P. Pai, R. Torro, M. Ludányi, P. Mélénec, M. Boughzala, V. Bertrand, P. Lenne
BioRxiv doi: https://doi.org/10.1101/2023.01.17.524363, 2023
Tissue patterning in embryos typically relies on diffusing proteins, called morphogens, that are
produced in one place, transported elsewhere, and then detected. Here, the authors study how Wnt ligands,
a family of signaling proteins, dynamically organize to establish cell polarity in a developing C.
elegans embryonic tissue. They used quantitative live imaging to show that Wnt ligands diffuse extracellularly
through the embryo over a timescale shorter than the cell cycle. Simulations supported this finding
and also showed how Wnt signaling can influence anterior versus posterior patterning. This work shows
how fast diffusion in the embryo can polarize target cells and supports diffusion-based long-range Wnt signaling.
|

|
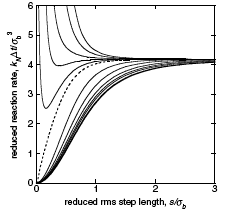
Maheshwari, A.J., A.M. Sunol, E. Gonzalez, D. Endy, R.N. Zia
mBio 14:e02865-22, 2023
As cells are fed more nutrients so that they grow faster, they clearly need to produce proteins at a faster rate.
However, it has been shown that they don't have a corresponding increase in the number of ribosomes, which implies
that each ribosome must produce proteins faster. These authors explored how this works using particle-based
simulations with "Colloidal Smoldyn", which is their extension of the Smoldyn software. In agreement with prior results,
they found that faster growth rates lead to greater macromolecular crowding within cells and that this affects reaction
rates in two opposing ways: rates increase due to higher effective reactant concentrations, and decrease due to
inhibited diffusion. They showed that the former effect dominates in this case, thereby answering the question of
how individual ribosomes are able to produce proteins faster with higher cell growth rates.
|
|
Guan, K., D.J. Lew, and T.C. Elston
PLOS Comp. Biol. 19:e1011523, 2023
This paper addresses the question of how cells are able to grow in correct directions with sufficient
versatility to reorient as needed, but also sufficient positive feedback to provide strong polarization. The
authors studied yeast cells, which orient their polarity sites up pheromone gradients in the course of mating.
A cell's initial polarity site is often oriented incorrectly, leading to a complicated reorientation process
that remains poorly understood. Particle-based simulations of the core polarity circuit revealed that
molecular-level fluctuations are insufficient for reorientation on their own but that inclusion of a
second pathway yielded results that agreed with experiments. This second pathway forms a positive feedback
loop involving the recruitment of receptors to the cell membrane, couples polarity establishment to gradient
sensing, and also allows cells to stabilize their final polarity site.
|
|
Mantovanelli, L., D.S. Linnik, M. Punter, H.J. Kojakhmetov, W.M. Smigiel, and B. Poolman
PLOS Comp. Biol. 19:e1011093, 2023
This paper describes a technique called Simulation-based Reconstructed Diffusion (SbRD), which determines
diffusion coefficients from microscope data by correcting for confinement effects and for the bias introduced
by two-dimensional models describing a three-dimensional motion. They validated the method on simulated diffusion
data. With SbRD, and a new cell detection method, the authors inferred the diffusion coefficients of
several native proteins in Escherichia coli, observing slower diffusion at the cell poles, and particularly
at old poles. They hypothesize that these effects are caused by aggregated or damaged proteins.
|
|
Opalko, H., S. Geng, A.R. Hall, D. Vavylonis, and J.B. Moseley
Mol. Biol. of the Cell mbc-E23, 2023
The authors investigated the localization of mitotic signaling proteins and the cytokinetic ring
in fission yeast cells. They studied the positioning of nodes, which are membrane-bound multiprotein
complexes and is important for timely cell cycle progression and positioning of the cytokinetic ring.
They combined experimental and modeling approaches to find that Cdr2 nodes accumulate near the nucleus,
and Cdr2 undergoes nucleocytoplasmic shuttling when cortical anchoring is reduced. Their model was supported
by particle-based simulations based on tip inhibition, nuclear positioning, and cortical anchoring.
|
|
Yonemura, Y., Y. Sakai, R. Nakata, A. Hagita-Tatsumoto, T. Miyasaka, and H. Misonou
BioRxiv doi: https://doi.org/10.1101/2023.04.26.538370, 2023
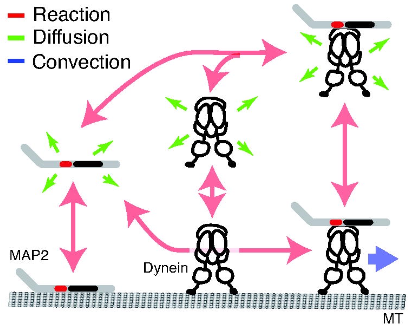
MAP2 is widely used as a neuronal dendrite marker but how its localization is established and maintained has
been unclear. The authors investigated how MAP2 is retained in the somatodendritic region using live
cell imaging with GFP-tagged MAP2. They found migration of MAP2 toward distal dendrites via transport
that depended on a serine-proline rich protein region. Inhibiting dynein showed that cytoplasmic dynein
is also involved in MAP2 transport, found to occur through dynein complex binding to MAP2. Modeling based on
experimental data confirmed that an intermittent active transport mechanism is essential (this modeling used
the Smoldyn version that runs within VCell). The authors conclude that cytoplasmic dynein recruits and
transports free MAP2 toward distal dendrites.
|
2022 |
|
|
Shaikh, B., L.P. Smith, D. Vasilescu, G. Marupilla, M. Wilson, ..., and J. Karr
Nucleic Acids Research 50: W108, 2022
Computational biology has struggled for many years with the wide variety of simulation tools, each with
its own format, algorithms, and interface. This paper described Biosimulators, which is a central registry
of simulation tools, with consistent Python, command-line, and containerized interfaces to each version
of each tool. BioSimulators is based on standards such as CellML, SBML, SED-ML, and the COMBINE archive
format. It supports BioNetGen, COPASI, NEURON, Tellurium, VCell, Smoldyn, and other simulators. See the
Biosimulators website.
|
|
Smigiel, W.M., L. Mantovanelli, D.S. Linnik, M. Punter, J. Silberberg, L. Xiang, K. Xu, and B. Poolman
Science Advances 8: eabo5387, 2022
This paper investigates the structure of the E. coli cytoplasm by experimentally tracking single proteins
using single-molecule displacement mapping. In this technique, the proteins are fluorescently labeled and
stroboscopically illuminated to create a list of displacements from one flash to the next. Results showed
that diffusion is slower near the cell poles and that it scales with the mass of the probes, but that it
is not affected substantially by native protein abundance. This suggests that the cytoplasm has subdomains
with varying perceived viscosities. The authors interpreted their experimental data using Smoldyn simulations.
|
|
Marquez-Lago, T.T. and S. Steinberg
Scientific Reports 12: 11791, 2022
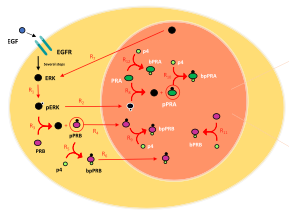
Progesterone receptors play key roles in the differentiation of the uterine endometrium, making progestin useful
for treating endometrial cancer. To better understand the roles of progesterone receptors in these contexts,
this work presents a spatial stochastic model to study the effects of progesterone receptor phosphorylation on
the levels of active transcription factor. These simulations confirm prior in vitro experiments, identifying
clustering as a central activating mechanism. This work was mostly performed in ChemCell, a simulator that is
conceptually similar to Smoldyn but has not been updated for many years, as a tribute to Alex Slepoy, who was one of
its authors. The simulation results were then confirmed with Smoldyn, which has been validated much more thoroughly.
|
|
Lyons, B., E. Isaac, N.H. Choi, T.P. Do, J. Domingus, J. Iwasa, A. Leonard, M. Riel-Mehan, E. Rodgers,
L. Schaefbauer, D. Toloudis, O. Waltner, L. Wilhelm, and G.T. Johnson
Nature Methods 19: 511, 2022
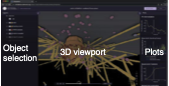
This paper introduces the Simularium viewer, which is a user-friendly open source application for sharing and
interrogating three-dimensional visualizations of biological simulation trajectories in a web browser. It's a
platform for sharing simulation outputs with an easy-to-use interface. This is especially important for spatial
modeling because these models tend to be complicated and, typically, not compatible with SBML or other standards
due to the wide variety of modeling frameworks that are used. The
Simularium website is compatible with models developed in Cytosim, PhsiCell, Smoldyn, SpringSaLaD, and
other simulators, and includes examples of each.
|
|
R. Taylor, J. Allard, and E.L. Read
Biophysical J. 121:1660, 2022
T cell signaling occurs when a close contact is formed between an antigen presenting cell and another cell,
and this close contact can only happen once the nearby CD45 molecules have diffused away from the region around
the T cell receptor. These authors studied the rate at which signaling can occur by simulating CD45 diffusion in
a "region of interest" (ROI) surrounding the T cell receptor. These simulations would be extraordinarily slow normally,
so the authors applied weighted ensemble averaging methods, shown in the diagram, to accelerate the simulations by
many orders of magnitude. This method distributes computational effort equally among the rare events (few molecules
in the ROI) and the common events (many molecules in the ROI).
|
|
Matveev, V.
Biophys. J. 121:4569-4584, 2022
Calcium-dependent cell processes are inherently stochastic due to large fluctuations in calcium channel gating
and other processes, but prior studies showed surprisingly close agreement between stochastic and deterministic
simulations. This paper investigates this result, showing that the close agreement arises from small correlations
between fluctuations of reactant molecule numbers, despite large fluctuation amplitudes. In the case
investigated here, diffusion and buffering effectively decorrelated the calcium sensor and calcium concentration
fluctuations.
|
|
Coulier, A., P. Singh, M. Sturrock, and A. Hellander
PLoS Comp. Biol. 18:e1010683, 2022
A persistent challenge in computational biology is in knowing what level of simulation detail is required to
adequately model a problem. More detail typically produces more accurate results, but at a large
computational cost, so it's generally better to use less detail when possible. These tradeoffs are particularly
challenging for model parameter estimation, which is already computationally intensive. This paper develops
a computational pipeline (see figure) that systematically evaluates model inference accuracy for a wide
range of true known parameters and then uses it to explore inference settings for negative feedback gene
regulation.
|
2021 |
|
|
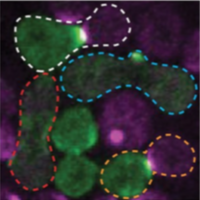
Clark-Cotton, M.R., N.T. Henderson, M. Pablo, D. Ghose, T.C. Elston, and D.J. Lew
Molecular Biology of the Cell 32:1048, 2021
Budding yeast cells use extracellular pheromone gradients to locate potential mating partners, which they
then grow toward. This work investigates how cells polarize, such as the fact that they often polarize in
unproductive directions initially, but then relocate their polarity sites until two partners' polarity sites align.
Polarity development is especially complicated in dense clusters of cells, which is also the situation that
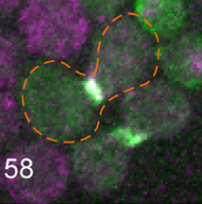
is most common in nature. This work is primarily experimental (the figure shows cells of opposite mating types
in green and purple, and an outlined fused zygote) but also used Smoldyn simulations, which suggested
that focal secretion at polarity sites is the central step in triggering commitment with the partner cell.
|

|
Ramirez, S.A., M. Pablo, S. Burk, D.J. Lew, T.C. Elston
PLoS Comp. Biol. 17: e1008525, 2021
Many cells direct their movement or growth toward external cues, such as budding yeast cells growing toward
potential mating partners in response to pheromone gradients. Within the cell, this directed growth is controlled
by polarity factors that assemble into clusters at the cell membrane. These clusters are highly dynamic,
with assembly, disassembly, and motion, before forming a stable polarity site that is directed toward the
pheromone source. These authors investigated this using their own computationally efficient RDME
(reaction-diffusion master equation) software, and validated their results using Smoldyn. Most simulations
focused on a planar 2D membrane surface, but some also used a spherical surface, as shown in the figure.
|
|
Saint-Sardos, A., S. Sart, K. Lippera, E. Brient-Litzler, S. Michelin, G. Amselem, C.N. Baroud
Small 16: 2002303, 2021
This paper describes a new experimental approach for measuring the secretions from individual spheroids of
human stem cells that are cultured within microfluidic droplets. It enables high-throughput quantification
by using a secondary droplet that brings functionalized micro-beads into proximity with each spheroid. Models,
performed with Smoldyn, investigated the molecular accumulation within the droplets and showed that physical
confinement is crucial for these measurements. The model also showed that the time to achieve a measurement
scales with droplet volume.
|
|
Coulier, A., S. Hellander, and A. Hellander
J. Chem. Phys. 154:184105, 2021
This paper describes a new simulation method for accelerating spatial simulations. It presents a multiscale model
where a compartment-based model approximates a detailed spatial stochastic model. The compartment model is constructed
via a first-exit time analysis on the spatial model, for which the authors used Smoldyn. The end result has
computational cost that is close to that of a stochasic well-mixed model. This new method is demonstrated
using the negative feedback loop for gene regulation that is shown in the diagram, showing substantial speed
improvements.
|
|
K.Y. Chen, E. Jenkins, M. Körbel, A. Ponjavic, A.H. Lippert, A.M. Santos, N. Ashman, C. O'Brien-Ball,
J. McBride, D. Klenerman, and S.J. Davis
Proc. Natl. Adac. Sci. USA 118:e2024250118, 2021
The authors used live cell imaging to investigate how T cell receptor (TCR) mobility affects T cell signaling.
They found that reduced mobility increases signaling. This suggests that trapping TCRs in tight cell-cell
interaction spaces might initiate T cell signaling, which extends the prior understanding that signaling was
tuned by TCR-ligand affinity. They used Smoldyn simulations, shown in the figure, to investigate TCR diffusion
for TCRs that were bound to different adducts, and then determining fractions of cells triggered from those
diffusion results.
|
|
Mott, R.E., C.R. von Reyn, B.L. Firestein, and D.F. Meaney
Frontiers in Comp. Neuroscience 15:580107, 2021
This paper investigates the role of neural activity on recovery after neural injury. It's mostly an
experimental paper, in which the authors applied microtrauma to in vitro neural tissues and imaged
the results with high speed calcium imaging. They found that neurons that were more active prior
to injury were more resistant to trauma and more likely to recover. They used Smoldyn simulations to
investigate changes in structure and calcium dynamics that would occur with random injury, using
a computational neural model that this group developed previously (Singh et al., 2011).
|
|
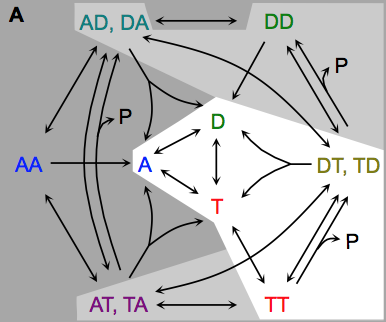
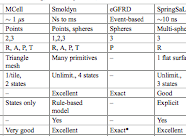
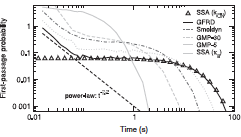
Johnson, M.E., A. Chen, J.R. Faeder, P. Henning, I.I. Moraru, M. Meier-Schellersheim, R.F. Murphy, T. Prustel, J.A. Theriot, A.M. Uhrmacher
Molecular Biology of the Cell 32:186, 2021
The authors review spatial stochastic simulation and then quantitatively compare several simulators using biological
problems of current interest. They used Virtual Cell for non-spatial and deterministic simulations, and NERDSS, Smoldyn,
MCell, and eGFRD for spatial stochastic simulations. All simulators worked well on most simple test cases (however,
Smoldyn was in error for 2D reaction rates, which are beyond the scope of the simulator at present). Other tests investigated
macromolecular crowding, as shown in the figure, the E. coli Min system, yeast polarization, and other systems. This paper
presents an excellent overview of where the field is currently and where it needs to go.
|
2020 |
|
|
Arjunan, S.N.V., A. Miyauchi, K. Iwamoto, and K. Takahashi
BMC Bioinformatics 21:33, 2020
Spatiocyte is a spatial stochastic simulation tool that uses a fine lattice, in which each lattice site
is occupied by up to one molecule at a time. These molecules can diffuse between sites or react with molecules
in neighboring sites. This paper describes a parallelized version of the software which is much faster than the
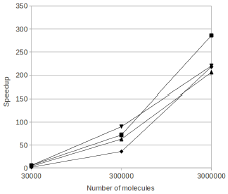
original serial version (which was already quite fast). The authors compared their results against Smoldyn,
finding that they got comparable results, thus verifying algorithm accuracy, and that their runtimes were 45
to 55 times faster than Smoldyn. This comparison used an 8 core computer, of which pSpatiocyte is optimized to
use all 8 cores, whereas Smoldyn only runs on 1 core.
|
|
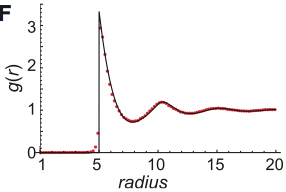
Johnston, S.T., C.N. Angstmann, S.N.V. Arjunan, C.H.L. Beentjes, A. Coulier, S.A. Isaacson, A.A. Khan, K. Lipkow, and S.S. Andrews
2018 MATRIX Annals 149-164, 2020
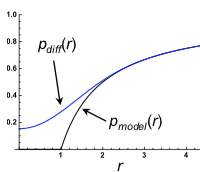
Smoldyn's standard bimolecular reaction algorithm is fast and leads to correct reaction rates, but is inaccurate
on very small size scales, while GFRD is more accurate but at the cost of high computational demands, begging
the question of whether new methods could be developed that are both accurate and fast. This paper develops
two such methods, both of which yield exactly correct radial distribution functions. However, they are still
sufficiently challenging to implement that these authors did not implement the methods in code, and nor are
these methods currently available in Smoldyn.
|
|
Andrews, S.S.
Phys. Biol. 17:045001, 2020
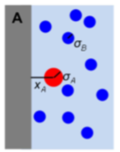
It is well known that macromolecular crowding affects the rates of bimolecular reactions through the effects that
volume exclusion accelerates reactions and diffusion inhibition slows reactions. This paper focuses on a third
effect, which is that crowders reduce access to reactants in their immediate vicinity. It shows this effect
first with a single reactant at a fixed distance from an impermeable surface, shown in the figure, and then
and then with a system crowded with immobile crowders. Accounting for this effect improves agreement between
analytical theory and simulations but is still somewhat in error, which prompted the author to explore other
models for macromolecular crowding as well. Those behaved differently, but had comparable size errors.
|
2019 |
|
|
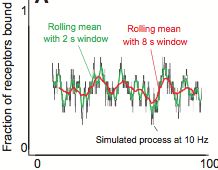
Henderson, N.T., M. Pablo, D. Ghose, M.R. Clark-Cotton, T.R. Zyla, J. Nolen, T.C. Elston, D.J. Lew
PLoS Biol. 17:e3000484, 2019
Yeast cells sense extracellular concentration gradients of pheromone molecules by determining which side of the
cell binds more pheromone molecules. This is challenging because yeast cells are small, there are few enough
receptors to create stochastic effects, and the receptors are not distributed evenly over the cell surface,
but yeast nevertheless accomplish it reliably. By combining experiments, such as shown in the figure, with
spatial simulations, the authors found that yeast cells detect the fraction of occupied receptors rather than
absolute numbers.
|
|
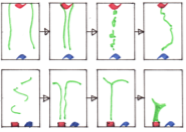
Thompson, S., P.D. Shipman, S.P. Shipman, and T.J. Zurlinden
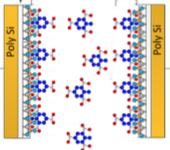
J. Chem. Phys. 150:154306, 2019
Vapor-phase ammonium chloride and hydrochloric acid react to form solid ammonium chloride. This paper
focuses on the patterns that ammonium chloride makes when the gasses diffuse together from separated sources,
such as some of those shown in the figure. The authors explored these patterns experimentally,
analytically, and with Smoldyn simulations. They found that the patterns arose from a moving reaction front,
combined with homogeneous (gas phase) and heterogeneous (on surfaces) nucleation.
|
2018 |
|
|
Chew, W., K. Kazunari, M. Watabe, S.V. Muniandy, K. Takahashi, and S.N.V. Arjunan
Phys. Rev. E 98:032418, 2018
Several different methods have been developed for running spatial simulations. These include continuous-
space and discrete-time, such as Smoldyn, continuous-space and continuous-time, such as EGFRD, and either
macroscopic or microscopic lattice-based methods. Microscopic lattice methods, in which each site is
about the size of one molecule, can be very fast but have had the drawback of not producing quantitatively
correct output. This paper addresses those issues by developing accurate microscopic lattice methods. The
authors tested their simulation results by comparing them with results from EGFRD and Smoldyn.
|
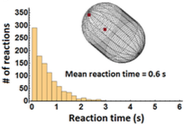
|
Schavemaker, P.E. A.J. Boersma and B. Poolman,
Frontiers in Molecular Biosciences 5:93, 2018
Although this paper doesn't directly answer the question posed in the title, it is nevertheless an excellent
introduction to the topics of intracellular diffusion and diffusion-limited reactions. It is also a
thorough review of experimental work in the fields. Relatively few chemical reactions in cells have
been shown to be diffusion-limited, but it appears that diffusion does limit overall cell growth, such as
by limiting protein elongation rates during protein synthesis. The authors used Smoldyn to estimate
the amount of time that a protein takes to diffuse within a cell before finding its target.
|
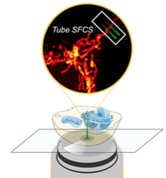
|
Unsay, J.D., F. Murad, E. Hermann, J. Ries, and A.J. Garcıa-Saez,
ChemPhysChem 19:3273, 2018
This paper introduces a new method for quantifying the diffusion and complex formation of fluorescently
labeled molecules in mitrochondrial compartments. It builds on two-focus scanning fluorescence correlation
spectroscopy (SFCS), in which fluorescently labeled molecules are observed in two different microscope
foci and the time correlation functions of the fluorescence in those two foci are used to compute diffusion
and interaction rates. This work extends SFCS to use in tubular structures, such as mitochondria. The authors
used Smoldyn simulations to check their results and eliminate possible candidate models.
|
|
Bianchi, F., L. Syga, G. Moiset, D. Spakman, P.E. Schavemaker, C.M. Punter, A. Seinen, A.M. van Oijen, A. Robinson, and B. Poolman,
Nature Comm. 9:501, 2018
Eukaryotic plasma membranes are complex structures, including eisosomes, which are recently discovered
immobile multi-protein complexes that mark the sites of endocytosis. These authors investigated protein
diffusion into and out of eisosomes with single protein microscopy. Their work suggests that the distinct
localization patterns found for several membrane proteins in S. cerevisiae arises from a combination of
slow lateral diffusion, steric exclusion, and conditional trapping in membrane compartments. They used
Smoldyn simulations to model their FRAP experiments.
|

|
D.B. Wilson, H. Byrne, and M. Bruna,
Phys. Rev. E 97:062137, 2018
This paper explores some of the effects of macromolecular crowding on diffusion, cellular chemotaxis,
and bimolecular reactions. The mathematical theories derived here agreed well with Smoldyn
simulations. The simulations used Smoldyn's excluded volume capabilities. In the figure shown at the left,
molecules diffused outward from an initial Gaussian profile, with different diffusion behaviors depending
on whether the molecules were treated with excluded volume or not.
|
|
Aguilar, B., A. Ghaffarizadeh, C.D. Johnson, G.J. Podgorski, I. Shmulevich, and N.S. Flann,
PLoS ONE 13:e0191089, 2018
Biofilm wrinkling is an interesting topic that may help build understanding about morphogenesis during
development. This work examines the hypothesis that the material properties of a biofilm both power and
control wrinkle formation within biofilms in response to localized cell death. This research did not use
the Smoldyn simulator but used the multi-cell Biocellion simulator instead. However, the authors used the
SmolCrowd utility to initially place their cells.
|
|
Li, X. and W.R. Holmes,
PLoS Comp. Biol. 14:e1005946, 2018
This study focuses on a calcium signaling pathway that is thought to be important for learning and memory,
which involves calcium, calmodulin, and the effector protein CaMKII. The authors modified Smoldyn so that
it could explicitly represent molecular binding and modification states, which enabled simple simulations
of the many different states of CamKII. Their experiments showed that CaMKII activity is sensitive to
calcium signal frequency and their models demonstrated how this frequency dependence relies on the amount
of calcium input, calmodulin availability, and the calcium diffusion rate.
|
2017 |
|
|
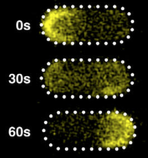
MacCready, J.S., J. Schossau, K.W. Osteryoung, and D.C. Ducat,
Mol. Microbiol. 103:483-503, 2017
The E. coli Min system, in which the MinC, MinD, and MinE proteins oscillate from pole to pole,
has become a model system for understanding emergent protein self-organization. These authors performed
the first study of Min oscillations in a different species, the cyanobacterium Synechococcus elongatus.
They found that the internal photosynthetic membranes in this species did not inhibit Min protein
oscillations and also suggested that Min protein affinity is greater for the plasma membrane.
|
|
Bates, J., I. Teh, D. McClymont, P. Kohl, J.E. Schneider, and V. Grau,
IEEE Transactions on Medical Imaging 36:1316-1325, 2017
Diffusion weighted magnetic resonance imaging (dwMRI) is a non-invasive technique for imaging with contrast
based on the diffusion of water molecules. These authors developed a model of dwMRI and validated it by
comparing simulations that were based on the model again experimental data from measurements of rat heart
cells. The found good agreement, based upon similar patterns in the eigenvalues of the diffusion tensor,
the mean diffusivity, and the fractional anisotropy.
|
|
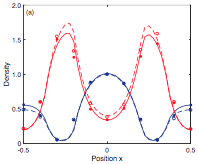
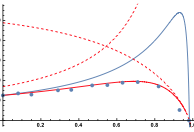
Wilson, D.B., H. Byrne, and M. Bruna,
ArXiv 1705.00004, 2017
This paper investigates the effects of macromolecular crowding on molecular diffusion and reactions.
It works towards the development of macroscopic models that can be computed efficiently using partial
differential equations but that are able to accurately capture the non-linear diffusion that occurs
at microscopic size scales. The figure shows that simuation data (points) agreed well with their
theory (lines). This work is highly mathematical.
|
|
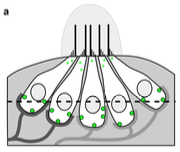
Graydon, C.W., U. Manor, and K.S. Kindt,
Scientific Reports 7:7467, 2017
Some auditory and visual sensory cells include structures called ribbons, which are composed primarily
of a protein called Ribeye. These authors studied diffusion of Ribeye within ribbons, focusing on hair
cells of zebrafish lateral lines (which are similar to hair cells in ears). They measured diffusion
using fluorescence recovery after photobleaching (FRAP) and then interpreted the results using Smoldyn
simulations.
|
|
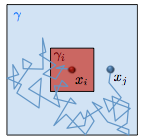
Meinecke, L.,
Bulletin of Math. Biol. 79:2672-2695, 2017
This paper presents a multiscale approach to modeling diffusion and reactions rates in a crowded environment.
The method combines jumping according to local first exit times and jumping on a coarser Cartesian grid. Excluded volume
is modeled by a diffusion equation with space-dependent diffusion coefficients. Simulations showed that crowding molecule
shape and size play a crucial role in the effects on diffusive motion. They also showed that molecular crowding can
enhance or inhibit chemical reactions depending on local obstacle density fluctuations.
|
2016 |
|

|
Jonas van den Berg, Heloisa Galbiati, Akiko Rasmussen, Samantha Miller, and Bert Poolman,
Scientific Reports 6:32709, 2016
Bacterial mechanosensitive channels protect cells from structural damage during hypoosmotic shock. The authors
combined physiological assays, quantitative photo-activated localization microscopy (qPALM), and quantitative simulations
to study them in E. coli. They found an almost linear relationship between channel abundance and cell survival. The MscL,
MscS, and MscK channelsdistribute homogeneously over the cytoplasmic membrane (see image) and diffuse in accordance with
their relative protein mass. However, MscL can also cluster when fluorescently tagged. These data help elucidate the biology
of mechanosensitive channels and emphasizes the need for care when using fluorescent tags.
|
|
Schaff, J.C. , F. Gao, Y. Li, I.L. Novak, and B.M. Slepchenko,
PLoS Comp. Biol. 12:e1005236, 2016
This paper describes the integration of the deterministic VCell simulator with the stochastic
Smoldyn simulator, both of which are spatial, to create the VCell hybrid solver. The resulting
simulator uses the same fixed time steps for both portions, and uses an overlapping space approach,
in which the solvers address different molecular species that are within the same physical region.
The hybrid solver is validated here with simple tests, and also illustrated with applications to
calcium sparks, stochastically gated reactions, and spontaneous cell polarization.
|
|
You, C., T.T. Marquez-Lago, C.P. Richter, S. Wilmes, I. Moraga, K.C. Garcia, A. Leier, and J. Piehler,
Science Advances 2:e1600452, 2016
Recent results have suggested that cell plasma membranes may be compartmentalized into small corrals or microcompartments
by the underlying membrane cytoskeleton. This paper combined experimental and simulation approaches to investigate the
consequences of those microcompartments on receptor dimerization. The authors showed that it stabilized receptor dimers
and caused dissociated receptors to reassociate rapidly, thus helping maintain signaling complexes.
|
|
Kondrat, S., O. Zimmermann, W. Wiechert, and E. von Lieres,
Eur. Phys. J. E 39:11, 2016
In many soft and biological physics applications, there are multiple distinct time and length scales.
For example, enzymes are large, move slowly, and are few, while metabolites are small, fast, and abundant.
The authors addressed this with a new hybrid simulation method, which is stochastic-deterministic and discrete-continuous.
They demonstrate it by modelling enzyme-catalysed reactions with discrete enzymes and continuous metabolites (see figure).
They validated their method by comparing simulation results from their new method against those from Smoldyn.
|

|
Meinecke, L. and M. Eriksson,
IET Systems Biology 11:55-64 2016
Simulations with off-lattice Brownian dynamics (e.g. Smoldyn) are computationally expensive in
crowded environments. This paper investigates the extent to which on-lattice simulations can
simulate reactions and diffusion in the presence of crowders. The authors show that diffusion is
slowed down in the off-lattice model since randomly distributed obstacles effectively exclude more volume than those
ordered on an artificial grid. Crowded reaction rates can be both increased and decreased by the grid structure. Grid
artifacts increase with increasing crowder density. The authors conclude that the computationally more efficient on-lattice
simulations are accurate only for low crowder densities.
|
2015 |
|
|
Andrews, S.S., S.N.V. Arjunan, G. Balbo, A.T. Bittig, J. Feret, K. Kaizu, and F. Liu,
In D. Gilbert, M. Heiner, K. Takahashi, and A.M. Uhrmacher, eds.
Multiscale Spatial Computational Systems Biology 170-187, 2015
The authors investigated the effect of macromolecular crowding on reaction rates using 5 different simulators,
both to develop a better understanding of the topic and to compare the simulators. The eGFRD algorithm was presumably
very accurate but ran very slowly, Smoldyn and NL-space worked well although Smoldyn appeared to
produce more accurate results, Spatiocyte was very fast but results had lattice artifacts, and KaSim worked, which was
remarkable because it is typically a non-spatial method. The Smoldyn results (figure) agreed with qualitative expectations
but showed that the theory that the authors investigated was incorrect.
|
|
Bates, J., I. Teh, P. Kohl, J.E. Schneider, and V. Grau,
Lecture Notes In Computer Science 9126:120-128, 2015
Diffusion MRI (magnetic resonance imaging) is a non-invasive experimental method for visualizing diffusion in tissues,
in this case in rat heart tissue. Here, the authors modeled this method using Smoldyn and found close correspondance
between model and experimental results. Next, they used the simulations to test the method sensitivity. They found
that the diffusivity has the greatest effect and the cross-sectional area and aspect ratio of cells are important, but
the cell length and volume fraction of cells had no marked effect.
|
|
Subburaj, Y., K. Cosentino, M. Axmann, E. Pedrueza-Villalmanzo, E. Hermann, S. Bleicken, J. Spatz, and A.J. García-Sáez,
Nature Comm. 6:8042, 2015
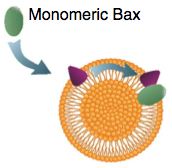
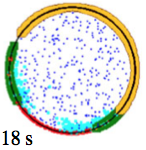
Bax is a key regulator of apoptosis, mediating cytochrome c release to the cytosol via oligomerization in the
outer mitochondrial membrane. These authors investigated the molecular mechanism of Bax assembly and regulation by
other Bcl-2 members. They found that Bax binds to the membrane in a monomeric state and then rapidly self-assembles.
They also show that other proteins, cBid and Bcl-xL, help drive Bax activity. Based on these experimental results, they
developed a theoretical model, using Smoldyn, which presents a new mechanism for the molecular pathway of Bax assembly
to form the apoptotic pore.
|
|
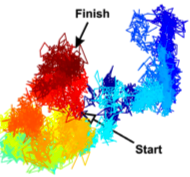
Xiaji Liu, Erik S. Welf, and Jason M. Haugh,
J. R. Soc. Interface 12:20141412, 2015
These researchers experimentally investigated T lymphocyte motility, which is similar to ameboid motility.
They found that cells typically turn by first creating a bifurcation of the lamellipodium at the cell's
leading edge and then following one of the new projections. They proposed a model of the major interactions
in this process. Simulation with Smoldyn (shown in the figure) agreed with their experimental results. The figure
shows the cell rear in beige and bifurcated actin regions in green.
|
|
Robert G. Endres,
PLoS ONE 10:e0121681, 2015
Many cell systems, including cell cycle ones and some signaling ones, are bistable. This has been studied most often
using deterministic and/or non-spatial models. This paper used Smoldyn models to investigate the more physiologically relevent case, which
is for stochastic chemical reactions in the confined 3-dimensional volume of a cell, considering both bacteria and
eukaryotic cells. The author finds that bistability is fragile in these conditions, often requiring finely tuned parameters,
small volumes, and fast diffusion coefficients. Switching can occur upon cell growth.
|
2014 |
|
|
Drago Strle,
Sensors 2014 IEEE 1320-1323, 2014
This work describes a model of a sensor system for vapor trace detection of molecules in the
air using an array of functionalised capacitive sensors and an electronic detection system. The author
simulated vapor diffusion, and adsorption and desorption to and from the sensors, using Smoldyn.
The resulting model makes it possible to study the interactions, selectivity, and sensitivity of the
sensor system in an efficient way, simplifying the design of sensor system modules for vapor trace
detection of different molecules in the air.
|
|
Hugo G. Schmidt, Sven Sewitz, Steven S. Andrews, and Karen Lipkow,
PLoS ONE 9:e108575, 2014
Transcription factors and other DNA binding proteins find their DNA binding sites faster than simple 3D diffusion allows.
These authors explored this acceleration with Smoldyn models. As in prior work, they found that non-specific DNA binding
followed by 1D sliding reduces finding times. They also found that intersegmental transfer, in which a transcription factor
that is non-specifically bound to DNA simultaneously binds a separate DNA loop and then releases the first binding site,
is also effective. Finally, they found that DNA binding proteins are enriched in dimers and tetramers, perhaps because this
favors intersegmental transfer.
|
|
Daniel E. Strongin, Mark Groudine, Joan C. Ritland Politz,
Nucleus 5:474-481, 2014
The genome is spatially organized within the eukaryotic nucleus. One aspect of this is that gene loci on different chromosomes
can preferentially colocalize. Using mouse strains that have different gene arragements on their chromosomes,
these authors investigated the driving force behind the colocalization of the IgH and Myc loci. They found
that it arose when both loci were on chromosomes that had nucleolar organizer regions (NORs). These are sites of ribosomal
DNA repeat sequences, which nucleate nucleoli. Together with simulations, these results implied that chromosome tethering
to nucleoli can help colocalize genes. The figure shows one chromosome in yellow, another in blue, and nucleoli in red,
in a strain where colocalization occurs.
|
|
H. Arthur Woods,
J. Experiment. Biol. 217:35-45, 2014
In this paper, the author proposes that stochastic variation during organismal development causes physiological
diversity within a single individual. He calls this mosaic physiology. This article reviews known mechanisms by which
stochastic effects arise in, and are controlled by, biological systems. It then goes on to show how then can give rise
to mosaic physiology. This provides a set of diversified phenotypes within single organisms, which may help the organism
to cope with novel environmental challenges. The figure shows stochastic effects in receptor-ligand binding, a simple
example of biological stochasticity.
|
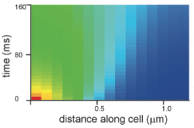
|
Jacek T. Mika, Paul E. Schavemaker, Victor Krasnikov, Bert Poolman,
Mol. Microbiol. 94:857-870, 2014
Proteins diffuse many times slower inside cells than they do in aqueous solutions due to macromolecular
crowding, non-specific binding, and hydrodynamic effects. This has been investigated most thoroughly in E.
coli, a Gram-negative bacterium. The authors investigated diffusion in L. lactis, a Gram-positive bacterium
here. They found similar diffusion coefficients and similar cell-to-cell variation in unstressed cells, but a smaller
increase upon osmotic challenge (as expected due to a higher turgor pressure). They measured intracellular diffusion with FRAP
methods, which they validated with Smoldyn simulations (figure).
|
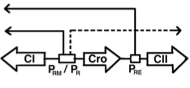
|
Matthew L. Robb and Vahid Shahrezaei,
PLOS One 9:e103636, 2014
Bacteriophage lambda is a classic system for studying cellular decision making. Upon infection, lambda can adopt the
lytic state in which it reproduces rapidly in the bacterium causing cell death and the release of virus, or it can adopt
the lysogenic state in which it incorporates itself into the cell genome; later, it may stochastically return to the lytic
state. This decision is made through a genetic switch, shown in the figure. These authors extended prior work by
investigating the role of the cell volume and bacterial growth rate on the decision. They also investigated spatial
effects, which arise primarily from the slow diffusion of mRNA across a bacterium (about 10 minutes), finding that
spatial effects were minimal.
|
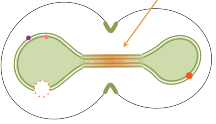
|
Eder Zavala and Tatiana T. Marquez-Lago,
PLoS Comp. Biol. 10:e1003725, 2014
Yeast cells retain their nuclear membranes during cell division, in a processs called closed mitosis. Membrane-bound proteins
segregate aysmmetrically in the process, with some getting localized in the mother cell and others in the bud (dots in
the figure). These authors explored mechanisms by which yeast cells might prevent protein diffusion across the division plane,
and hence maintain the localization. They found that a combination of protein rings and sphingolipid domains is
necessary during early anaphase, but that sphingolipid domains alone are adequate during late anaphase (figure), due to the
elongated nuclear neck.
|
2013 |
|
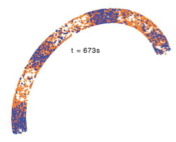
|
Max Hoffmann and Ulrich S. Schwarz,
Soft Matter 10:2388, 2014
One way in which E. coli bacteria find their mid-planes, so that cell division yields two equal size daughter
cells, is with spatiotemporal oscillations of the Min proteins. These proteins oscillate from pole to pole, with
minimal occupancy of the mid-plane. The simplicity and remarkable dynamics of this system has made it popular for
spatial stochastic simulations. These authors investigated Min system operation in artificial micropatterned environments
and in mutant filamentous cells, such as the one shown in the figure. This work highlights the robustness and variability
of Min system oscillations, puts limits on the effect of putative division sites, and provides a computational framework
for future studies.
|
|
Steven A. Frank,
Biology Direct 8:31, 2013
This paper discusses relations among Michaelis-Menten kinetics, the Hill equation, and biological information processing.
A central question that the paper probes regards why Michaelis-Menten kinetics leads to linear input-output relations
for low signal levels, but the Hill equation exhibits logarithmic sensitivity at these levels. This paper has numerous
misconceptions and non-standard terminology but nevertheless presents some intriguing points. A particularly interesting
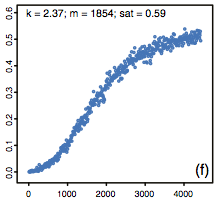
result is that dose-response curve for the Michaelis-Menten reaction, which normally exhibits Hill equation behavior with Hill
coefficient of 1, becomes ultrasensitive when reactions are substantially diffusion influenced, as shown in the figure.
|
|
Meghan McCabe Pryor, Shalini T. Low-Nam, Ádám M. Halász, Diane S. Lidke, Bridget S. Wilson, and Jeremy S. Edwards,
Biophys. J. 105:1533-1543, 2013
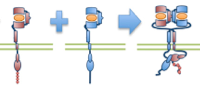
ErbB1 (epidermal growth factor receptor) is an important receptor for growth and development, and its overexpression can
cause cancer. These authors built on their prior erbB1 single molecule tracking experiments to build a spatial stochastic model for erbB1
diffusion, dimerization, kinase activation, and phosphorylation. The figure shows erbB1 dimerization. The model yields new
insight into the activation states of individual erbB1 monomers. For the most part, the authors used their own reimplementation of Smoldyn's
algorithms, although they also used the Smoldyn for part of the research as well.
|
|
Günther Gerisch, Mary Ecke, Ralph Neujahr, Jana Prassler, Andreas Stengl, Max Hoffmann, Ulrich S. Schwarz and Eberhard Neumann,
J. Cell Science 127:4507-4517, 2013
Electric pulses induce Dictyostelium discoideum cells to fuse. The authors combined electron microscopy,
fluorescence microscopy, and simulation to study the fusion pores and actin localization that arise in the membrane
during cell fusion. They found that the plasma membranes of the contiguous cells become tangles of highly bent and
interdigitated membranes. By imaging GFP diffusion from one cell to its neighbor, and then modeling this diffusion with
Smoldyn simulations as shown in the figure, they found that membranes persist in a fusogenic state for up to 24 seconds
before pores of about 3 nm are formed. |
2012 |
|

|
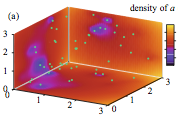
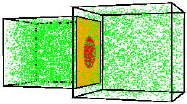
T.T. Marquez-Lago, A. Leier, and K. Burrage,
IET Syst. Biol. 6:134-142, 2012
The study compares both fractional Brownian motion and continuous time random walks and highlights how
well they can represent different types of spatial crowding and physical obstacles. Although diffusion around
immovable obstacles could be reasonably characterised by a single Hurst exponent, the authors found that diffusion in
a crowded environment seemed to exhibit multifractional properties in the form of a different short- and
long-time behaviors. The figure shows a 2-dimensional crowded environment, developed with the Smoldyn utility
program SmolCrowd. |
|
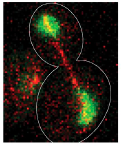
Barbara Boettcher, Tatiana T. Marquez-Lago, Mathias Bayer, Eric L. Weiss, and Yves Barral,
J. Cell Biol. 197:921-937, 2012
The authors investigated the establishment and maintenance of asymmetric cell division in budding yeast. Here,
unlike in mammalian cells, the nuclear envelope is maintained during cell division, and divides at about the same
time as the cell membrane. Using photobleaching and Smoldyn simulations, they found that diffusion barriers
compartmentalize the nuclear membranes, whereas protein diffusion was well explained by the dumbbell shape of the
anaphase nucleus. The figure shows a dividing cell with the nucleoplasmic GFP in green and mCherry-Tub1 spindles
in red.
|

|
Khan, S., T.S. Reese, N. Rajpoot, and A. Shabbir, J. Comput. Neurosci.
33:123-139, 2012
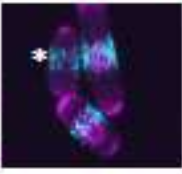
The authors investigated the sequestration of calcium calmodulin dependent kinase (CaMKII) in neural
dendritic spines, which is a key cellular mechanism for the formation and storage of memories. The
figure shows confocal microscopy data of GFP-CamKII localization shortly the GFP was photo-activated at
the asterisk; bright green regions, such as at the spine tip, indicate CamKII sequestration, while red
regions indicate low CamKII concentrations. Smoldyn simulations showed that a major cause of sequestion
is the high number of cytoskeletal binding sites at spine tips, rather than high binding affinities.
|
2011 |
|
|
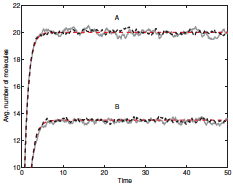
Leier, A. and T.T. Marquez-Lago, J. Chem. Phys. 135:134109, 2011
The two primary methods for simulating chemical reactions and diffusion are continuous-space single particle
methods, like Smoldyn uses, and lattice-based reaction-diffusion master equation (RDME) methods. The
latter are typically more efficient but can suffer from several artifacts. In this work, the authors presented
an accurate RDME method for simulating reactive boundary conditions, which they validated using Smoldyn.
The figure shows simulation results from their methods in black, analytical results in red, and Smoldyn
results in gray.
|

|
Jilkine, A., S.B. Angenent, L.F. Wu, and S.J. Altschuler, PLoS Comput. Biol.
7:e1002271, 2011
Many cell types, including budding yeast, mammalian neutrophils, and amoeba, can spontaeously polarize in
the absence of spatial cues. The authors propose that this polarization arises from positive feedback; it
robustly maintains an off state at low concentrations of signaling molecules, and then switches to highly
localized signaling clusters at higher concentrations. The figures show that in their model, increasing
signaling molecule concentrations (right panel vs. left panel) leads to clusters of molecules that are in
their active states (red).
|
|
Singh, P., A.J. Hockenberry, V. Tiruvadi, and D.F. Meaney, PLoS Comput. Biol.
7:e1002106, 2011
Neural NMDA receptors mediate many physiological functions, including the molecular basis for learning and
memory. These receptors exist in various subtypes, which enables them to discriminate between different types
of signals. Using Smoldyn models, the authors found that different receptors have different
dynamic ranges, that specific subtypes dominate in long-term depression and long-term potentiation situations,
and that the content of a specific subtype enhances response magnitude and fidelity during long-term potentiation.
The yellow and red portions of the figure show pre- and post-synaptic regions, while dots represent receptors.
|

|
Khan, S., Y. Zou, A. Amjad, A. Gardezi, C.L. Smith, C. Winters, T.S. Reese, J. Comput.
Neurosci. 31:581-594, 2011
This work investigated the sequestration of calcium dependent kinase II (CamKII) in neural dendritic spines
following synaptic stimulation. It looked at the effects of spine geometry on CamKII diffusion, binding of
CamKII to the post-synaptic density, to the cytoskeleton, and to other CamKII proteins. Simulation results
compared favorably with microscopy experiments. This work showed that self-aggregation of CamKII could provide
a switch that amplifies CamKII sequestration and regulates its activity.
|
|
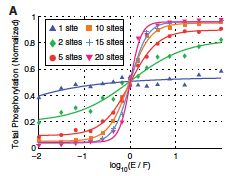
Dushek, O., P.A. van der Merwe, and V. Shahrezaei, Biophys. J. 100:1189-1197, 2011
The authors showed that multiple phosphorylation sites on a single protein
can produce switch-like responses when reactions between proteins are limited by diffusion.
This is the case for many reactions that occur on the plasma membrane. The figure shows that
ultrasensitivity increases with as the number of protein phosphorylation sites increase.
Smoldyn file.
|
2010 |
|
|
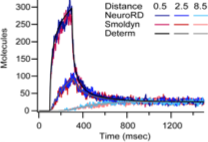
Oliveira, R.F., A. Terrin, G. Di Benedetto, R.C. Cannon, W. Koh, M. Kim, M. Zaccolo, and K.T. Blackwell,
PLoS ONE 5:e11725, 2010
This work investigates mechanisms that increase the local concentration of cyclic AMP (cAMP), which is essential for
normal neural functioning, including for synaptic plasticity. To do so, the authors developed a new spatial simulator
called NeuroRD, which is a compartment-based simulator. It combines the spatial Gillespie method with tau-leaping and
a new diffusion algorithm. The authors validated NeuroRD by comparing results against mass action theory and against
Smoldyn simulations. These comparisons are shown in the figure.
|
|
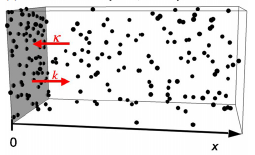
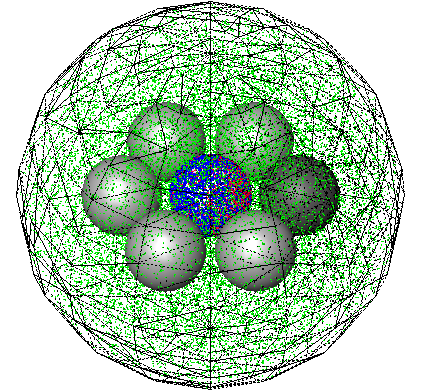
Andrews, S.S., N.J. Addy, R. Brent, and A.P. Arkin, PLoS Comp. Biol. 6:e1000705, 2010
The authors investigated mating pheromone signaling between yeast cells. A central "receiver" cell is covered
with receptors that bind mating pheromone, which is secreted by surrounding "sender" cells (in the figure, unbound
receptors are blue, bound receptors are red, and pheromone is green). This work showed that the central cell can better
locate strong pheromone emitting cells when the central cell secretes a pheromone-degrading protease because
the protease cloud sharpens the local pheromone gradient.
|
2009 |
|
|
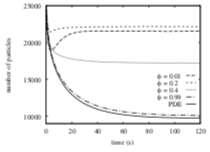
Palm, M.M., M.N. Steijaert, H.M.M. ten Eikelder, and P.A.J. Hilbers Proceedings of the Third International Conference on the Foundations of Systems Biology in Engineering, 2009
This paper focuses on molecule adsorption and desorption at surfaces, comparing results from PDE type
and particle-based simulations. When they began their work, Smoldyn placed desorbed molecules at the
surface, which the authors showed to disagree with PDE results. Smoldyn was improved during the course
of this work to place desorbed molecules at the correct distance from the surface, which the authors
showed led to excellent agreement with PDEs. This paper also shows that stochastic simulations are needed
when there are relatively few individual molecules.
|
|
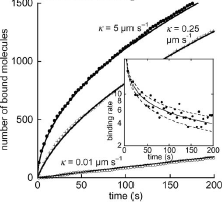
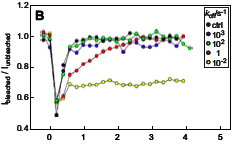
DePristo, M.A., L. Chang, R.D. Vale, S.M. Khan, and K. Lipkow, Prog. Biophys. Mol. Biol. 100:25-32, 2009
The authors used simulations to analyze and quantify experimental Fluorescence Recovery After Photobleaching
(FRAP) data for proteins in the E. coli chemotaxis system. They quantified protein diffusion
coefficients of 2 μm2/s and assessed turnover rates between
cytoplasmic proteins and membrane-associated protein clusters. The figure shows simulated CheY-YFP fluorescence in
a protein cluster as it is photobleached and then recovers from protein exchange. In general, simulations
can be useful tools for the quantitative analysis of fluorescent microscopy experiments.
|
2008 |
|
|
Lipkow, K. and D.J. Odde, Cell. Mol. Bioeng. 1:84-92, 2008
Using simulations, the authors showed that several of the E. coli chemotaxis proteins (CheY and CheZ)
likely have stable protein concentration gradients across the length of cells. This arises from protein activation
that is localized to one cell pole and activation-dependent protein complexation that affects protein
diffusion coefficients. These mechanisms, and similar ones, occur for many other proteins as well, so stable
protein concentration gradients within cells are likely to be widespread.
|
2006 |
|
|
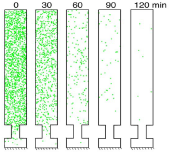
Grati, M., M.E. Schneider, K. Lipkow, E.E. Strehler, R.J. Wenthold, and B. Kachar,
J. Neuroscience 26:6386-6395, 2006
This work combined experimental and modeling approaches to investigate membrane protein turnover in stereocilia
(fine hairs in the inner ear that convert mechanical motion to electrical signals) to better understand
stereocilia recovery from trauma, such as loud noises. The authors focused on the spatial distribution, mobility,
and trafficking of the PMCA2 protein, which is both abundant and essential to stereocilia function. They found
that PMCA2 exhibits rapid turnover, which supports other evidence that stereocilia undergo rapid continuous renewal.
The figure shows PMCA2 (green dots) distribution on an unrolled stereocilia membrane over time.
|
|
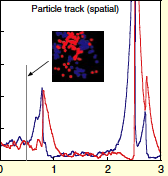
Andrews, S.S. and A.P. Arkin, Current Biology 16:R523-R527, 2006
This is a primer on how to simulate cell biology systems. It presents the basics of ODE (ordinary differential
equation) modeling, stochastic modeling, spatial modeling, and spatial-stochastic modeling. Of particular
interest, it presents simulations of the same Lotka-Volterra predator-prey system that used each of the different
methods. The results differ dramatically. Deterministic simulations show nearly sinusoidal oscillations,
non-spatial stochastic simulations show oscillations with increasing amplitudes, and particle-tracking
(Smoldyn; figure show here) simulations show a characteristic boom-and-bust pattern.
|
|
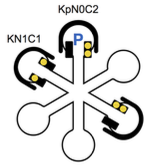
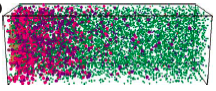
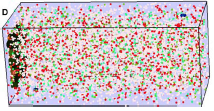
Lipkow, K., PLoS Comp. Biol. 2:e39, 2006
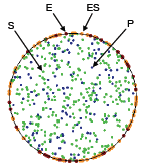
In the E. coli chemotaxis system, the CheY messenger protein is phosphorylated at a receptor
cluster near one cell pole and is dephosphorylated by the CheZ protein. The author used simulations
to explore the signaling behaviors that arise with different CheZ localizations. She found that the model
that best agreed with experiments included CheZ proteins that oligomerize and localize to the receptor
cluster upon cellular stimulation. The black dots in the figure are CheZ oligomers (also, pink dots are CheY, red
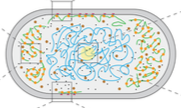
are CheYp, and green are non-oligomeric CheZ). This creates a negative feedback loop which improves
system precision, robustness, and adaptation.
|
2005 |
|
|
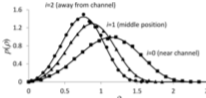
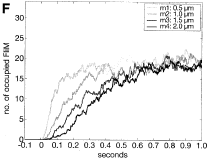
Lipkow, K., S.S. Andrews, and D. Bray, J. Bact. 187:45-53, 2005
The authors developed a spatial stochastic simulation of the central E. coli chemotaxis system. It
includes the core proteins and reactions, a polar-localized receptor cluster, and several flagellar motors
in the cell membrane. Increasing cytoplasmic crowding, due to ribosomes and other macromolecules, resulted
in slower protein diffusion, steepened concentration gradients, and substantial differences in signal
propagation delays to motors at different positions (figure).
|